Here, we provide standard definitions for mathematical functions and properties
that are used throughout this repository.
Implementation of these definitions are found within the individuals modules,
as well as python scripts found with the utilities folder ‘util’ within the ‘wlcstat’
repository.
Coordinate Definitions
Here, we define coordinate systems and transformations of coordinate systems
Spherical coordinates
Spherical coordinate system is defined such that
\[x = r \sin \theta \cos \phi, \hspace{0.2in}
y = r \sin \theta \sin \phi, \hspace{0.2in}
z= r \cos \theta\]
The unit triad in spherical coordinates (relative to cartesian coordinates) is given by
\[\begin{split}& &
\hat{\delta}_{r} =
\sin \theta \cos \phi \hat{\delta}_{x} +
\sin \theta \sin \phi \hat{\delta}_{y} +
\cos \theta \hat{\delta}_{z}
\nonumber \\
& &
\hat{\delta}_{\theta} =
\cos \theta \cos \phi \hat{\delta}_{x} +
\cos \theta \sin \phi \hat{\delta}_{y} -
\sin \theta \hat{\delta}_{z}
\nonumber \\
& &
\hat{\delta}_{\phi} =
-\sin \phi \hat{\delta}_{x} +
\cos \phi \hat{\delta}_{y}\end{split}\]
Gradient, Divergence, Curl, and Laplacian are given by
\[\begin{split}& &
\vec{\nabla} \psi =
\hat{\delta}_{r} \frac{\partial \psi}{\partial r}+
\hat{\delta}_{\theta} \frac{1}{r} \frac{\partial \psi}{\partial \theta}+
\hat{\delta}_{\phi} \frac{1}{r \sin \theta} \frac{\partial \psi}{\partial \phi}
\nonumber \\
& &
\vec{\nabla} \cdot \vec{A} =
\frac{1}{r^{2}} \frac{\partial ( r^{2} A_{r})}{\partial r}+
\frac{1}{r \sin \theta} \frac{\partial ( A_{\theta} \sin \theta)}{\partial \theta}+
\frac{1}{r \sin \theta} \frac{\partial A_{\phi}}{\partial \phi}
\nonumber \\
& &
\vec{\nabla} \times \vec{A} =
\hat{\delta}_{r}\frac{1}{r \sin \theta } \left( \frac{\partial (A_{\phi} \sin \theta)}{\partial \theta} -
\frac{\partial A_{\theta}}{\partial \phi} \right) +
\hat{\delta}_{\theta} \frac{1}{r} \left( \frac{1}{\sin \theta} \frac{\partial A_{r}}{\partial \phi} -
\frac{\partial (r A_{\phi})}{\partial r} \right) +
\hat{\delta}_{\phi} \frac{1}{r} \left( \frac{\partial (r A_{\theta})}{\partial r} - \frac{\partial A_{r}}{\partial \theta} \right)
\nonumber \\
& &
\nabla^{2} \psi =
\frac{1}{r^{2}} \frac{\partial}{\partial r} \left( r^{2} \frac{\partial \psi}{\partial r} \right) +
\frac{1}{r^{2} \sin \theta } \frac{\partial }{\partial \theta} \left( \sin \theta \frac{\partial \psi}{\partial \theta} \right) +
\frac{1}{r^{2} \sin^{2} \theta } \frac{\partial^{2} \psi}{\partial \phi^{2}}\end{split}\]
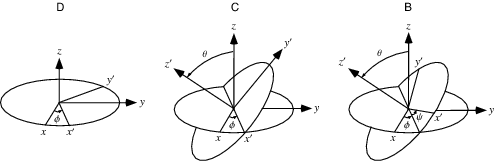
Rotations by Euler angles
We represent a 3D rotation operation using Euler angles \(\phi, \theta, \psi\). We define the rotation matrix
\(\mathbf{R}(\phi, \theta, \psi)\) according the three successive rotation matrices, given by
\[\mathbf{R}(\phi, \theta, \psi) = \mathbf{B}(\psi) \cdot \mathbf{C}(\theta) \cdot \mathbf{D}(\phi)\]
where
\[\begin{split}\mathbf{D}(\phi) =
\begin{bmatrix}
\cos \phi & \sin \phi & 0 \\
- \sin \phi & \cos \phi & 0 \\
0 & 0 & 1
\end{bmatrix}\end{split}\]
\[\begin{split}\mathbf{C}(\theta) =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \theta & \sin \theta \\
0 & - \sin \theta & \cos \theta
\end{bmatrix}\end{split}\]
\[\begin{split}\mathbf{B}(\psi) =
\begin{bmatrix}
\cos \psi & \sin \psi & 0 \\
- \sin \psi & \cos \psi & 0 \\
0 & 0 & 1
\end{bmatrix}\end{split}\]
The
Spherical Harmonics
We define the spherical harmonics \(Y_{l}^{m}\)
accordingly to [Arfken1999].
The spherical harmonics form a complete basis set
for the 3-dimensional angular Laplacian \(\vec{\nabla}_{u}^{2}\).
The range of the indices \(l\) and \(m\) are \(l \in [0, \infty]\) and \(m \in [-l, l]\).
We define the spherical harmonics
as
\[Y_{l}^{m} (\theta, \phi) =
\sqrt{\frac{2l + 1}{4 \pi} \frac{(l-m)!}{(l+m)!}}
P_{l}^{m} ( \cos \theta) e^{i m \phi}\]
where \(P_{l}^{m} (\rho)\) are the associated Legendre polynomials.
The spherical harmonics satisfy
\[\int d \vec{u} Y_{l}^{m} (\vec{u})
Y_{l'}^{m'*}(\vec{u}) = \delta_{ll'} \delta_{mm'}\]
This definition for spherical harmonics forms a complex-valued basis set.
The tesseral spherical harmonics \(Y_{lm}\) are also used in this repository,
forming a real-valued basis set that is convenient in some applications.
The tesseral spherical harmonics are defined as
\[\begin{split}& & Y_{lm} =
\left\{
\begin{array}{c}
\frac{i}{\sqrt{2}} \left( Y_{l}^{m} - (-1)^{m} Y_{l}^{-m} \right)
\hspace{0.5in} \mathrm{if} \, \, m < 0
\\
Y_{l}^{0}
\hspace{1.9in} \mathrm{if} \, \, m = 0
\\
\frac{1}{\sqrt{2}} \left( Y_{l}^{m} + (-1)^{m} Y_{l}^{-m} \right)
\hspace{0.5in} \mathrm{if} \, \, m > 0
\end{array}
\right.\end{split}\]
Rotation of spherical harmonics
For many calculations, we need to evaluate the rotated spherical harmonics.
We define \(\vec{u}'\) as the orientation vector \(\vec{u}\) rotated by the
Euler angles \(\alpha\), \(\beta\), and \(\gamma\).
The spherical harmonic \(Y_{l}^{m}(\vec{u}')\) is determined to be
\[Y_{l}^{m}(\vec{u}') = \sum_{m' = -l}^{l} \mathcal{D}_{l}^{m m'}(\alpha, \beta, \gamma)
Y_{l}^{m'}(\vec{u})\]